
文章首发于「陈树义」公众号及个人博客 shuyi.tech
树是一种非常实用的数据结构,最常用的就是数据库的索引,用于在海量数据查找目标值。举个例子,如果你的表有 1 亿的数据。如果使用链表来存储,那么你最坏情况下需要遍历 1 亿次才能找到目标值。
但如果你使用红黑树来查找,那你最坏情况下的时间复杂度为 O(logN),即最坏只需要 27 次就可以找到。27 次查找与 1 亿次的查找,这中间相差了 300 万倍,由此可见树结构带来的效率提升之巨大!
那我们应该如何去学习树这种数据结构呢?
其实树这种数据结构也是有其知识体系的,每一种树结构的诞生都有其原因及实际场景。我们需要找到这种场景,梳理出一条主线,将这些知识点串起来,形成一个知识体系。 例如我们所知道的树结构有:
- 树
- 二叉树
- 二叉查找树
- 二叉平衡树
- AVL树
- 红黑树
- B-树
- B+树
- 树堆
- 2-3树
- 伸展树
- Trie树
- 字母树
- 哈夫曼树
- 等等
关于树的数据结构数不胜数,让我们眼花缭乱。但在这么多树结构中,我梳理出了一条主要的核心链路。这条核心链路涵盖了我们日常最长使用的树结构,并且它们之间还是关联密切的,这条链路我取名叫:树结构大道!
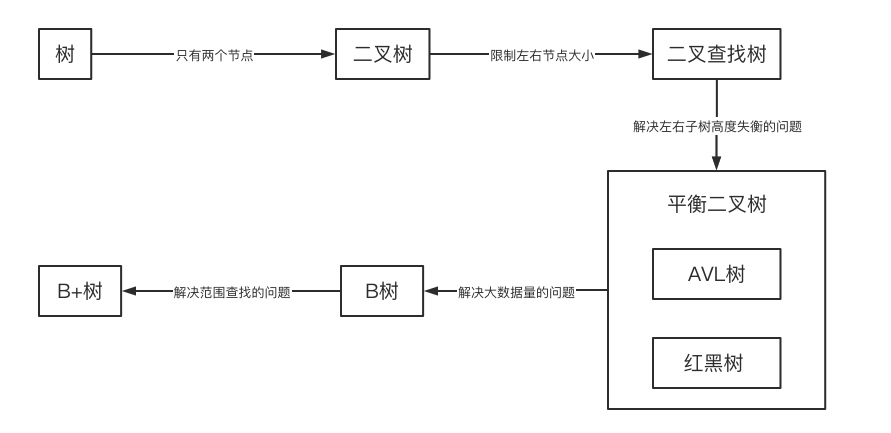
树结构大道开始于最基础的树的定义,它最为简单、没有过多的限制。在树定义的基础上,如果我们限制每个节点最多有两个子树,那么它就变成了二叉树。在二叉树的基础上,如果我们限制左节点要小于本节点、右节点要大于本节点,那么它就变成了二叉查找树(BST)。
二叉搜索树在最坏的情况下会演变成链表,即二叉搜索树的左右子树失衡了(根节点的左边一个节点都没有,所有节点都偏向右边了)。而我们都知道树的查找效率取决于树的高度,如果演变成链表,那么查找效率就从 O(logN) 变成了 O(N)。为了控制左右子树的高度,就诞生了平衡二叉树这种结构。平衡二叉树就是用来解决二叉查找树失衡问题的。
我们最常听见的 AVL 树和红黑树,其实都是平衡二叉树,只不过它们的侧重点不同。AVL树侧重于查询多、增删少的场景,因此其平衡度较高。而红黑树侧重于增删频繁的场景,因此其平衡度较低。
平衡二叉树基本上能解决绝大多数的问题,但此时又有一次问题诞生了。如果我们的树结构很大,有几十亿的数据,我们如何去搭建一颗平衡二叉树?最常见的是数据库一个表几十亿的数据,我们如何对其进行排序?如果直接将数据加载到内存,那么内存势必会爆表,不可行。
此时 B 树(B-Tree)诞生了!
B 树采用磁盘块的方式解决了数据存储空间的问题。简单地说,使用平衡二叉树时我们的树节点每次只能比较一个值。如果有几十亿个节点,那我们就必须往内存中加载几十亿个数字,构建几十亿个树节点。而 B 树的一个节点对应了一个磁盘块,而这一个磁盘块有 4KB 大小的数据,这样我们所构建的树节点规模就缩减了 4K 倍之巨!B 树通过增加每个节点的数据数量,减少了加载到内存的数据大小、树的高度,从而解决了平衡二叉树在大数据量查找时的可行性及效率问题。
但 B 树还有一个问题,及它在范围查找方面性能很差。
此时 B+ 树(B+ Tree)诞生了!
B+ 树在 B 树的基础上,在每个根节点添加一个向右的指针,可以直接获取到下一个元素。通过这种方式,我们只需要找到查找范围里最小的元素之后,再做一次链表查询就可以了,极大地提高了查询效率。简单地说,B+ 树通过叶节点的指针,解决了 B 树范围查找效率慢的问题。
看到这里,我们的「树结构大道」基本上结束了。我们从最基础的树结构出发,一路经过二叉树、二叉查找树、平衡二叉树(AVL树、红黑树)、B树、B+树。通过它们的诞生背景及应用场景,将它们串了起来。
经过这么一梳理,你会发现我们所说的内容已经涵盖大部分日常知识点。那么剩下的知识点怎么办呢?我的建议是遇到的时候单独了解,然后将其添加到我们的知识体系中。 到目前为止,我的树结构知识体系如下图所示:
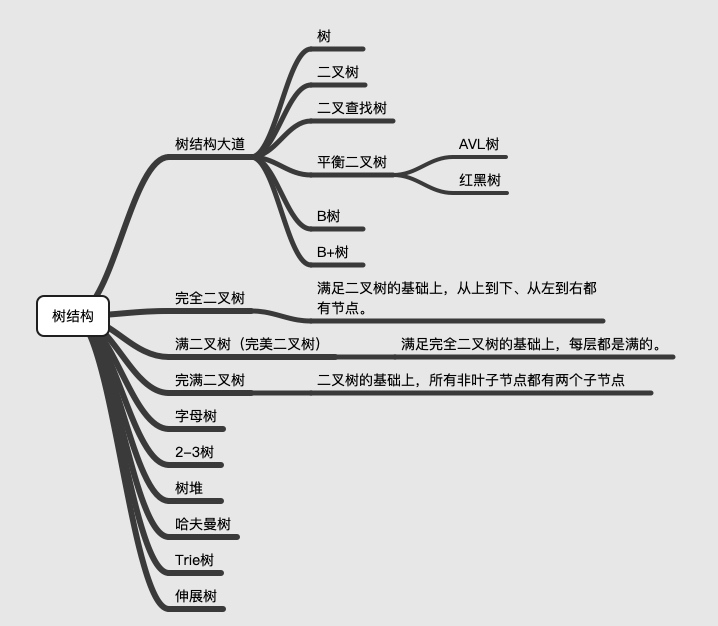
接下来几篇文章,我将详细带大家游览「树结构大道」,欢迎大家关注~